Es el proceso matemático de encontrar el ritmo al cual una función trigonométrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sin(x), cos(x) y tan(x).
A continuación mencionare dos de las funciones trigonométricas derivadas:
Derivada de la funcion seno
La Derivada del seno de una función es igual al coseno de la función por la derivada de la función.
A partir de la definición de la derivada de una función f(x):
Por tanto si f(x) = sin(x)
A partir de la identidad trigonométrica sin(A + B) = (sin(A)cos(B) + cos(A)sin(B), se puede escribir
Agrupando los términos cos(x) y sin(x), la derivada pasa a ser
Reordenando los términos y el límite se obtiene
Ahora, como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener
El valor de los límites
Por tanto, si f(x) = sin(x),
Derivada de la funcion coseno
La derivada del coseno de una función es igual a menos seno de la función por la derivada.
Si f(x) = cos(x)
A partir de la identidad trigonométrica cos(A + B) = cos(A)cos(B) − sin(A)sin(B), se puede escribir
Operando se obtiene
Como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener
El valor de los límites
Son 1 y 0 respectivamente. Por tanto, si f(x) = cos(x),
 Video ExplicativoEn este video te mostremos como se pueden derivar las funciones trigonometricas, se desarrollaran algunos ejercicios para lograr la practica del tema.Ejercicios practicosAquí te presentamos algunos ejercicios para ejercitar el uso del tema:
Video ExplicativoEn este video te mostremos como se pueden derivar las funciones trigonometricas, se desarrollaran algunos ejercicios para lograr la practica del tema.Ejercicios practicosAquí te presentamos algunos ejercicios para ejercitar el uso del tema:














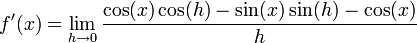



y como sa hacen las derivas en los cosenos
ResponderEliminarcogiendo los seno de tu mama ajjaja
Eliminarjsjsjsj c mamo :V
Eliminaralguien mme podria decir como se realiza la derivada de una funcion
ResponderEliminarno
Eliminar